Menentukan jumlah n suku pertama deret geometri dan Menentukan berbagai pemfaktoran
Indikator Soal : Menentukan jumlah n suku pertama deret geometri, jika unsur yang diperlukan diketahui
Diketahui barisan bilangan 3, 6, 12, 24, ….. Jumlah 10 suku pertama barisan itu adalah...
A. 2012
B. 2024
C. 3023
D. 3069
Kunci Jawaban: D
Pembahasan:
Diketahui a = 3, r = 2, dan n = 10
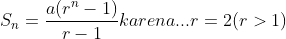
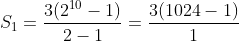
= 3 x 1023
Jadi jumlah 10 suku pertama = 3069
Indikator Soal : Menentukan berbagai pemfaktoran
Dari pemfaktoran berikut:
1. 4x2 – 36 = (2x- 6) (2x + 6 )
2. 4x2 – 7x - 2 = (2x -1) (2x + 2 )
3. x2 – 4 = (x + 2) (x - 2)
4. x2 – 4x = 2x(x - 2)
yang benar adalah …
A. 1 dan 3
B. 1 dan 4
C. 2 dan 3
D. 2 dan 4
Kunci Jawaban: A
Pembahasan:
1. 4x2 –36 = (2x- 6) (2x+ 6 ) ...... (B)
2. 4x2 – 7x - 2 = (4x +1)(x-2) .......(S)
3. x2 – 4 = (x + 2) (x - 2) ...........(B)
4. x2 – 4x = x(x - 4) ...................(S)
Untuk lebih jelasnya pembahasan mengenai berbagai bentuk pemfaktoran dari bentuk aljabar dapat dilihat dari penjelasan dibawah ini.
ax ± ay = a (x ± y) → a bisa koefisien atau variabel
Contoh Soal :
2x + 10y = 2(x + 5y) → a sebagai koefisien
4x - 4y = 4(x - y) → a sebagai variabel
b. Pemfaktoran dalam bentuk selisih kuadrat
x2 - y2 = (x + y) (x - y)
Contoh Soal :
x2 - 52 = (x + 5) (x - 5)
c. Pemfaktoran dalam bentuk kuadrat sempurna
x2 + 2xy + y2 = (x + y)2
x2 - 2xy + y2 = (x - y)2
Contoh Soal :
x2 + 10x + 25 = (x + 5)2
x2 - 10x + 25 = (x - 5)2
d. Pemfaktoran dalam bentuk ax2 + bx + c = 0, dimana a = 1
ax2 + bx + c = (x + m) (x + n)
dengan m + n = b | m x n = c
Contoh Soal :
x2 + 9x + 18 = (x + 3) (x + 6)
karena 3 + 6 = 9 | 3 x 6 = 18
m = 6 dan n = 3 atau m = 3 dan n = 6
e. Pemfaktoran dalam bentuk ax2 + bx + c = 0, dimana a ≠ 1
a x c = m x n dan m + n = b
Contoh Soal :
2x2 + 3x + 1 = 0
2 x 1 = m x n dengan syarat m + n = 3
yang memenuhi adalah m = 2 dan n = 1
maka : 2x2 + 3x + 1 = 0 menjadi 2x2 + 2x + x + 1 = 0
→ 2x(x + 1) + 1(x + 1) = 0
→ (2x + 1) (x + 1)
Soal : Menentukan jumlah n suku pertama deret geometri
Indikator : Menyelesaikan masalah yang berkaitan dengan barisan bilangan dan deret.Indikator Soal : Menentukan jumlah n suku pertama deret geometri, jika unsur yang diperlukan diketahui
Diketahui barisan bilangan 3, 6, 12, 24, ….. Jumlah 10 suku pertama barisan itu adalah...
A. 2012
B. 2024
C. 3023
D. 3069
Kunci Jawaban: D
Pembahasan:
Diketahui a = 3, r = 2, dan n = 10
= 3 x 1023
Jadi jumlah 10 suku pertama = 3069
 |
| Menentukan jumlah n suku pertama deret geometri dan Menentukan pemfaktoran |
Soal : Menentukan berbagai pemfaktoran
Indikator : Menentukan pemfaktoran bentuk aljabar.Indikator Soal : Menentukan berbagai pemfaktoran
Dari pemfaktoran berikut:
1. 4x2 – 36 = (2x- 6) (2x + 6 )
2. 4x2 – 7x - 2 = (2x -1) (2x + 2 )
3. x2 – 4 = (x + 2) (x - 2)
4. x2 – 4x = 2x(x - 2)
yang benar adalah …
A. 1 dan 3
B. 1 dan 4
C. 2 dan 3
D. 2 dan 4
Kunci Jawaban: A
Pembahasan:
1. 4x2 –36 = (2x- 6) (2x+ 6 ) ...... (B)
2. 4x2 – 7x - 2 = (4x +1)(x-2) .......(S)
3. x2 – 4 = (x + 2) (x - 2) ...........(B)
4. x2 – 4x = x(x - 4) ...................(S)
Untuk lebih jelasnya pembahasan mengenai berbagai bentuk pemfaktoran dari bentuk aljabar dapat dilihat dari penjelasan dibawah ini.
Menentukan pemfaktoran bentuk aljabar
a. Pemfaktoran dalam bentuk distributifax ± ay = a (x ± y) → a bisa koefisien atau variabel
Contoh Soal :
2x + 10y = 2(x + 5y) → a sebagai koefisien
4x - 4y = 4(x - y) → a sebagai variabel
b. Pemfaktoran dalam bentuk selisih kuadrat
x2 - y2 = (x + y) (x - y)
Contoh Soal :
x2 - 52 = (x + 5) (x - 5)
c. Pemfaktoran dalam bentuk kuadrat sempurna
x2 + 2xy + y2 = (x + y)2
x2 - 2xy + y2 = (x - y)2
Contoh Soal :
x2 + 10x + 25 = (x + 5)2
x2 - 10x + 25 = (x - 5)2
d. Pemfaktoran dalam bentuk ax2 + bx + c = 0, dimana a = 1
ax2 + bx + c = (x + m) (x + n)
dengan m + n = b | m x n = c
Contoh Soal :
x2 + 9x + 18 = (x + 3) (x + 6)
karena 3 + 6 = 9 | 3 x 6 = 18
m = 6 dan n = 3 atau m = 3 dan n = 6
e. Pemfaktoran dalam bentuk ax2 + bx + c = 0, dimana a ≠ 1
a x c = m x n dan m + n = b
Contoh Soal :
2x2 + 3x + 1 = 0
2 x 1 = m x n dengan syarat m + n = 3
yang memenuhi adalah m = 2 dan n = 1
maka : 2x2 + 3x + 1 = 0 menjadi 2x2 + 2x + x + 1 = 0
→ 2x(x + 1) + 1(x + 1) = 0
→ (2x + 1) (x + 1)